Graph Exploration with Apache Hadoop and MapReduce

Hi all,
sometimes you will have data where you don’t know how elements of these data are connected. This is a common usecase for graphs, this is because they are really abstract.
So if you don’t know how your data is looking like, or if you know how it looks like and you just want to determine various graph components, this post is a good chance for you to get the “MapReduce-way” of graph exploration. As already mentioned in my previous post, I ranted about message passing through DFS and how much overhead it is in comparison to BSP.
Just let this be a competition of Apache Hama BSP and Apache Hadoop MapReduce. Both sharing the HDFS as a distributed FileSystem.
Looking at the title you know that this post is about the MapReduce implementation, I write a BSP implementation later and compare this with this MapReduce implementation.
Let’s introduce the prequisites now.

Prequisites
We have a graph in a format of an adjacency list looking like this:

0  
1    4    7  
2    3    8  
3    5  
4    1  
5    6  
6  
7      
8    3  
9    0  

So the first entry on the left side is always the vertex, therefore all vertices are listed on the leftmost side. Each vertex is described by a number: its id.
Separated by tabs are the vertex ids that are adjacent to the vertex on the leftmost side.

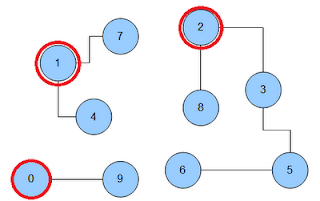
This is quite abstract so let’s take a look at this pretty picture:

This is how this graph looks like. As you can see there are three components: [1,4,7];[2,3,5,6,8];[0,9].
In some datasets you want to classify each component to a common key that is unique. In this case it is the most common solution to just let a component be classified by its lowest id. E.G the component [1,4,7] has the lowest id 1. It is the classifier for this component.

How do we deal with this in MapReduce?
First of all I recommend you to read into this paper. It describes a technique named “message passing”.
Simple: The idea behind this is, that you let the vertices pass messages if a new local minima has been found. Afterwards you are just merging the messages with the real vertices and apply updates on the vertices that had a higher minimum.

So our first task is to write the value class that is representing a vertex AND a message at the same time.

public class VertexWritable implements Writable, Cloneable {  
  
 LongWritable minimalVertexId;  
 TreeSet<LongWritable> pointsTo;  
 boolean activated;  
          
public boolean isMessage() {  
  if (pointsTo == null)  
   return true;  
  else  
   return false;  
 }  
  
}  

And the typical read/write stuff coming with Writable.
So let me explain to you, we have this class representing the Vertex: it has a pointsTo tree that will maintain the adjacent vertex ids and the currently minimalVertexId. And there is also a boolean field that is called “activated”.
There is also a method that determines whether this is representing a message or a vertex.

The whole thing is just working like this:

1. Import the vertices from the adjacency list to the ID mapped to Vertex form.
2. In the first iteration flag every vertex as activated and write it again.
3. If a vertex is activated, loop through the pointsTo tree and write a message with the (for this vertex) minimal vertex to every element of the tree.
4. Merge messages with the related vertex and if we found a new minimum activate the vertex. If nothing was updated then deactivate it.

And then repeat from point 3 until no vertex can be updated anymore.
Part 1 and 3 are inside the Map Task, part 2 and 4 are reduce tasks.
Look here how you can implement a job recursion using Apache Hadoop.

So after all iteration is done you’ll have the following output:

 0 | VertexWritable \[minimalVertexId=0, pointsTo=\[0\]\]  
 1 | VertexWritable \[minimalVertexId=1, pointsTo=\[1, 4, 7\]\]  
 2 | VertexWritable \[minimalVertexId=2, pointsTo=\[2, 3, 8\]\]  
 3 | VertexWritable \[minimalVertexId=2, pointsTo=\[3, 5\]\]  
 4 | VertexWritable \[minimalVertexId=1, pointsTo=\[1, 4\]\]  
 5 | VertexWritable \[minimalVertexId=2, pointsTo=\[5, 6\]\]  
 6 | VertexWritable \[minimalVertexId=2, pointsTo=\[6\]\]  
 7 | VertexWritable \[minimalVertexId=1, pointsTo=\[7\]\]  
 8 | VertexWritable \[minimalVertexId=2, pointsTo=\[3, 8\]\]  
 9 | VertexWritable \[minimalVertexId=0, pointsTo=\[0, 9\]\]  

So you see that we always have every vertex on the left side, but now the minimalVertexId is the classifier for the component. And we have the three lowest component identifiers found: 0,1 and 2!

So this looks like that now:

If you are now interested in getting all vertices to a component identifier you’ll be able to write a new mapper that will extract the minimalVertexId as a key and the pointsTo elements as a value. So that in the reduce step they’ll be merged together and you can persist your data.

And if you are interested in more source code you are free to look into my Summer of Code project under: http://code.google.com/p/hama-shortest-paths/
You’ll find a working algorithm inside of the package called “de.jungblut.mapreduce.graph”. The main function to call is inside the class “DatasetImporter.java”.
The example input used in this post is also in the trunk. So check this out and you are welcome to use it for your own problems ;)

So the next time I write a BSP that will do the same.